Signal modeling

Back to top

This page describes the functions Gannet uses to model metabolite signals. Note that when the definition of a parameter is omitted from a table under a particular metabolite, it is implied that it has been defined already in a previously described function.

For all model fitting, Gannet uses nonlinear regression, with fit parameters optimized using the least-squares Levenberg-Marquardt algorithm. For increased computational speed and a better solution, the starting values of the optimization are derived from a “pre-fit” that uses the trust-region-reflective algorithm. Description of these algorithms can be found in the online MATLAB documentation.

GABA+Glx

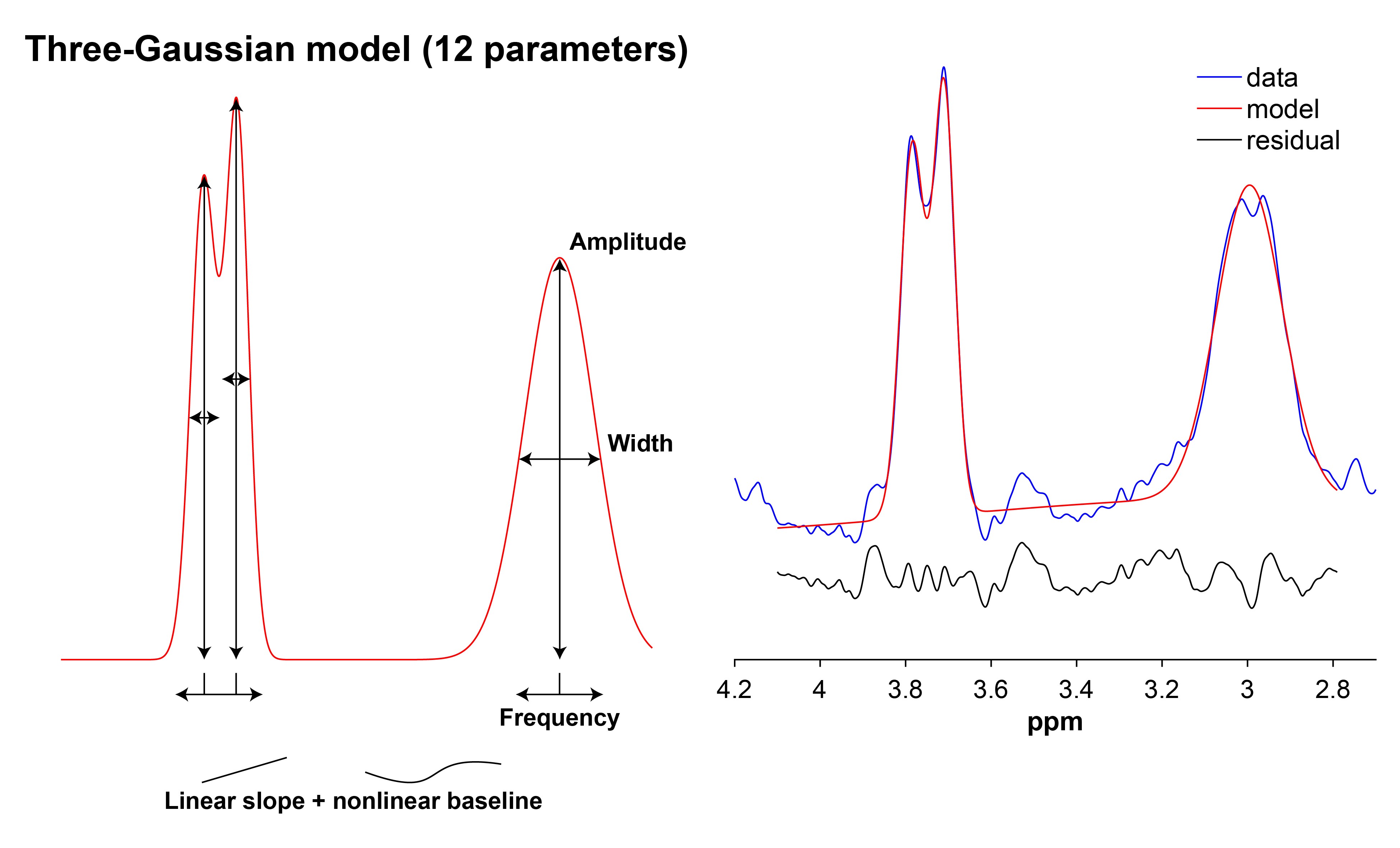
GABA and Glx are fitted using a three-Gaussian model with a linear slope and non-linear baseline:

\[ S(f) = \sum_{i=1}^{3}\left\{A_i\exp[\sigma_i(f-f_i)^2]\right\}+ m(f-f_1)+ b_1\sin(\pi{f}/1.31/4)+ b_2\cos(\pi{f}/1.31/4) \]

where:

Parameter	Definition
\(f\)	Frequency (ppm)
\(A_i\)	Gaussian i’s amplitude
\(\sigma_i\)	Gaussian i’s width
\(f_i\)	Gaussian i’s center frequency (ppm)
\(m\)	Slope of linear baseline
\(b_1\)	Sine baseline term
\(b_2\)	Cosine baseline term

  The GABA+Glx model is fitted using a model that has observation weights between 3.16 and 3.285 ppm, where the Cho subtraction artifact¹ appears. The purpose is to down-weight the influence of this artifact (if present) on the model fitting.

GSH (TE < 100 ms)

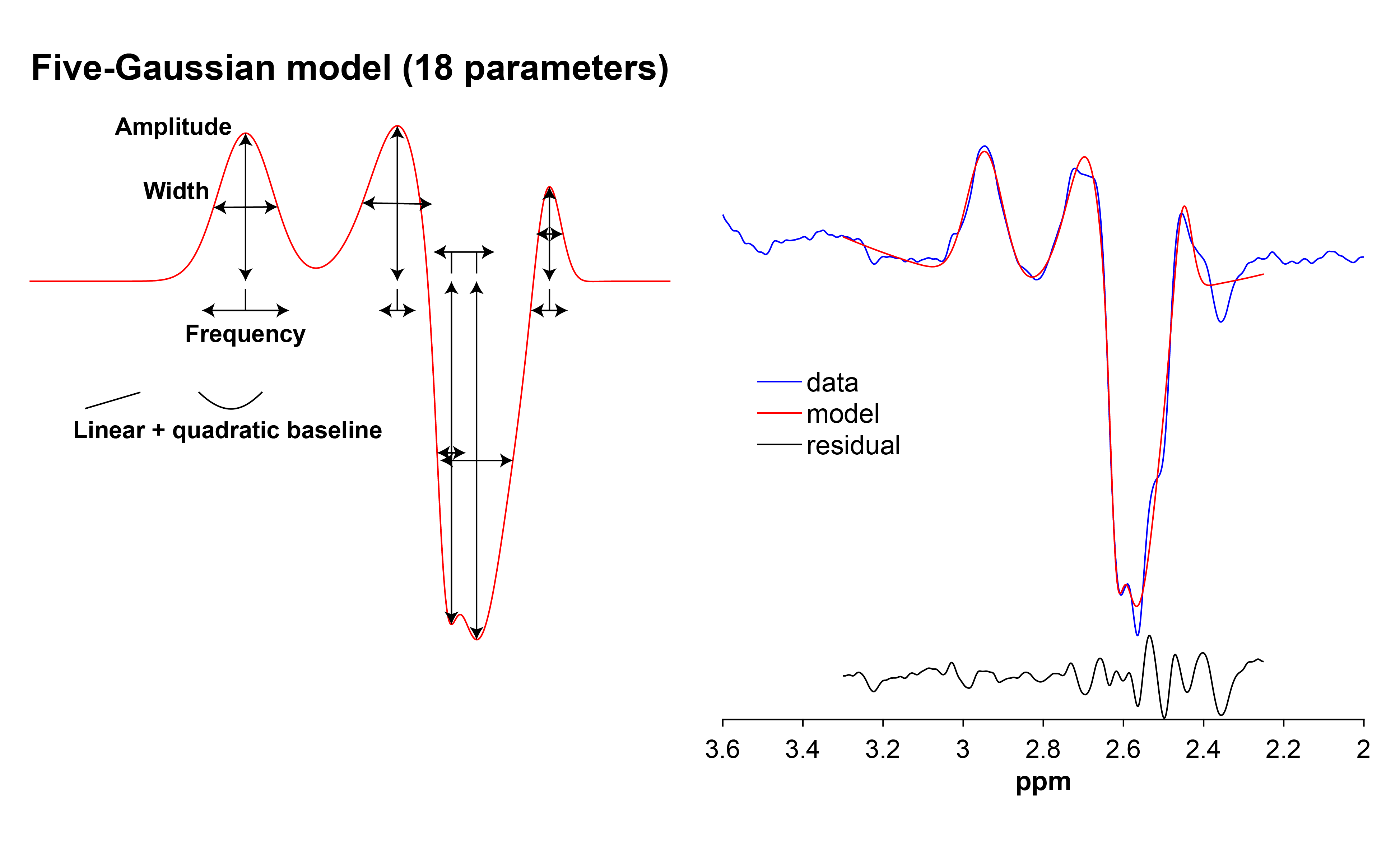
GSH that is edited at a TE < 100 ms is fitted with a five-Gaussian model with a linear + quadratic baseline:

\[ S(f) = \sum_{i=1}^{5}\left\{A_i\exp[\sigma_i(f-f_i)^2]\right\}+ m_1(f-f_1)+ m_2(f-f_1)^2+b \]

where:

Parameter	Definition
\(m_1\)	Slope of linear baseline
\(m_2\)	Quadratic baseline term
\(b\)	Baseline offset

GSH (TE >= 100 ms)

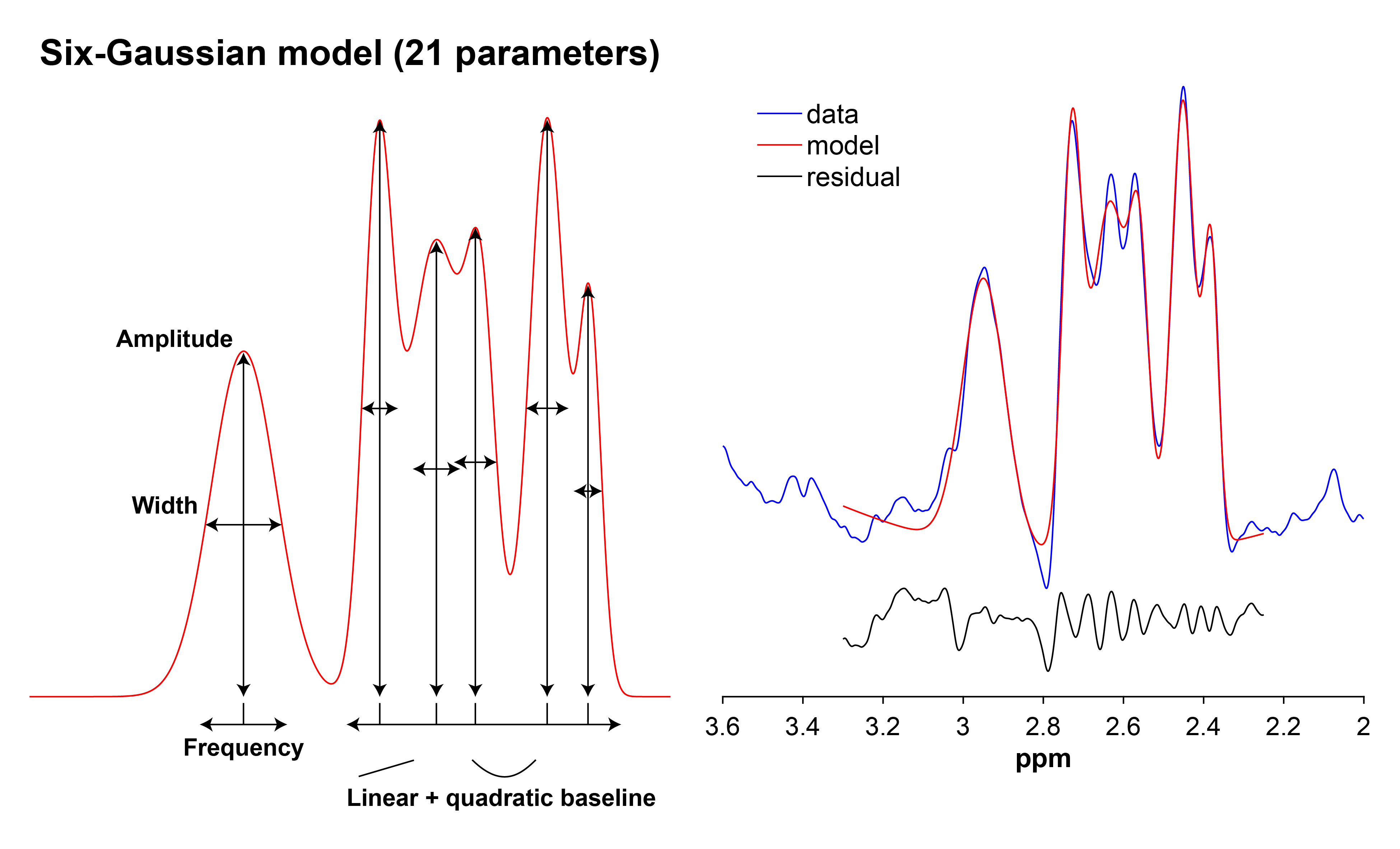
GSH that is edited at a TE >= 100 ms is fitted with a six-Gaussian model with a linear + quadratic baseline:

\[ S(f) = \sum_{i=1}^{6}\left\{A_i\exp[\sigma_i(f-f_i)^2]\right\}+ m_1(f-f_1)+ m_2(f-f_1)^2+b \]

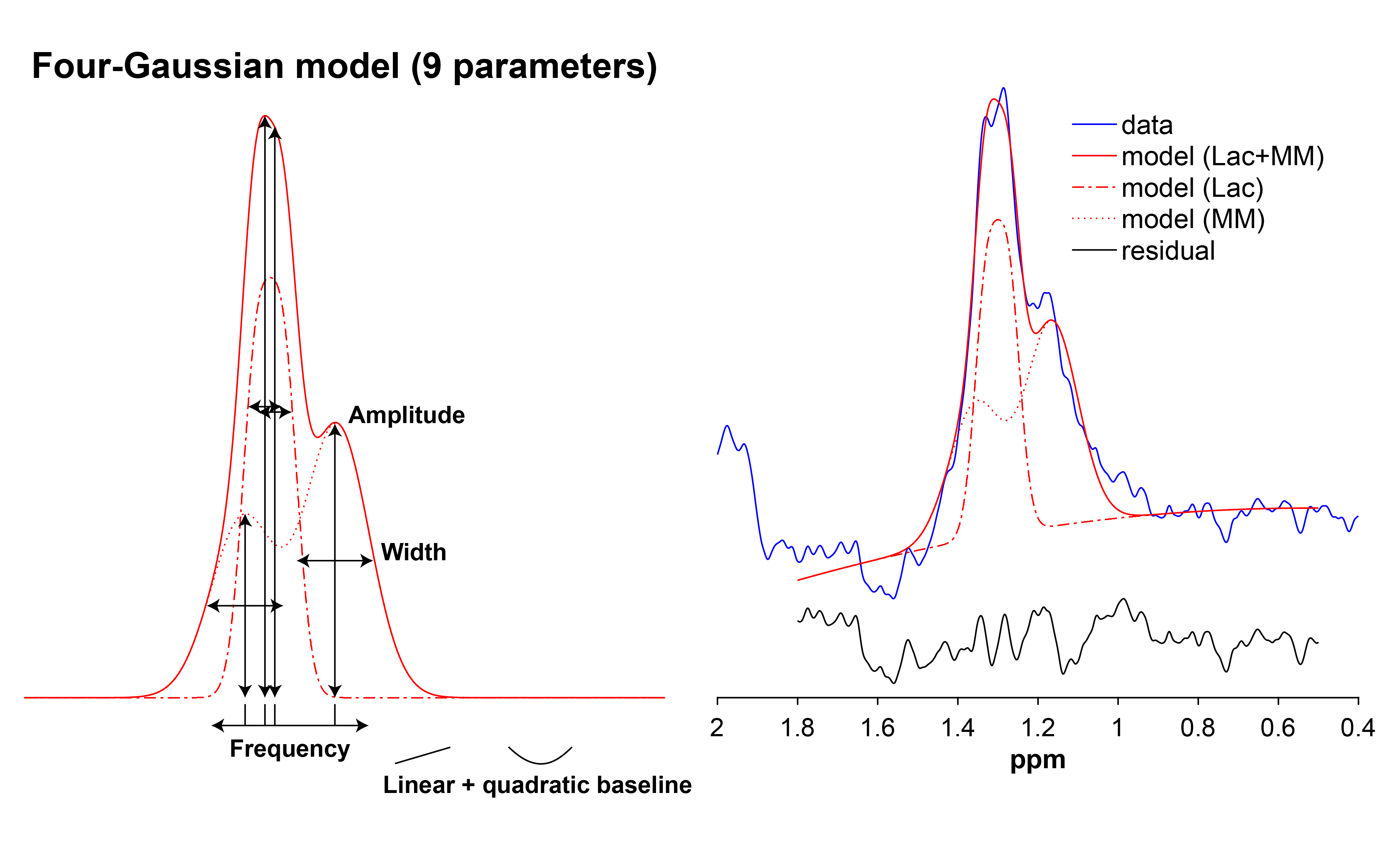
Lac

Model optimization of the edited Lac peak is ongoing.

Lac is fitted with a four-Gaussian model with a linear + quadratic baseline:

\[ S(f) = \sum_{i=1}^{4}\left\{A_i\exp[\sigma_i(f-f_i)^2]\right\}+ m_1(f-f_1)+ m_2(f-f_1)^2+b \]

EtOH

EtOH is fitted with a two-Lorentzian model with a linear baseline:

\[ S(f) = \sum_{i=1}^{2}\left[\frac{A_{i}}{1+\left(\frac{f-f_{i}}{\gamma_{i}/2}\right)^2}\right]+ m(f-f_1)+b \]

where:

Parameter	Definition
\(A_i\)	Lorentzian i’s amplitude
\(f_i\)	Lorentzian i’s center frequency (ppm)
\(\gamma\)	Lorentzian width (full-width at half-maximum)

  The EtOH model is fitted using a model that has observation weights between 1.29 and 1.51 ppm, where the Lac subtraction artifact appears. The purpose is to down-weight the influence of this artifact (if present) on the model fitting.

Cho+Cr

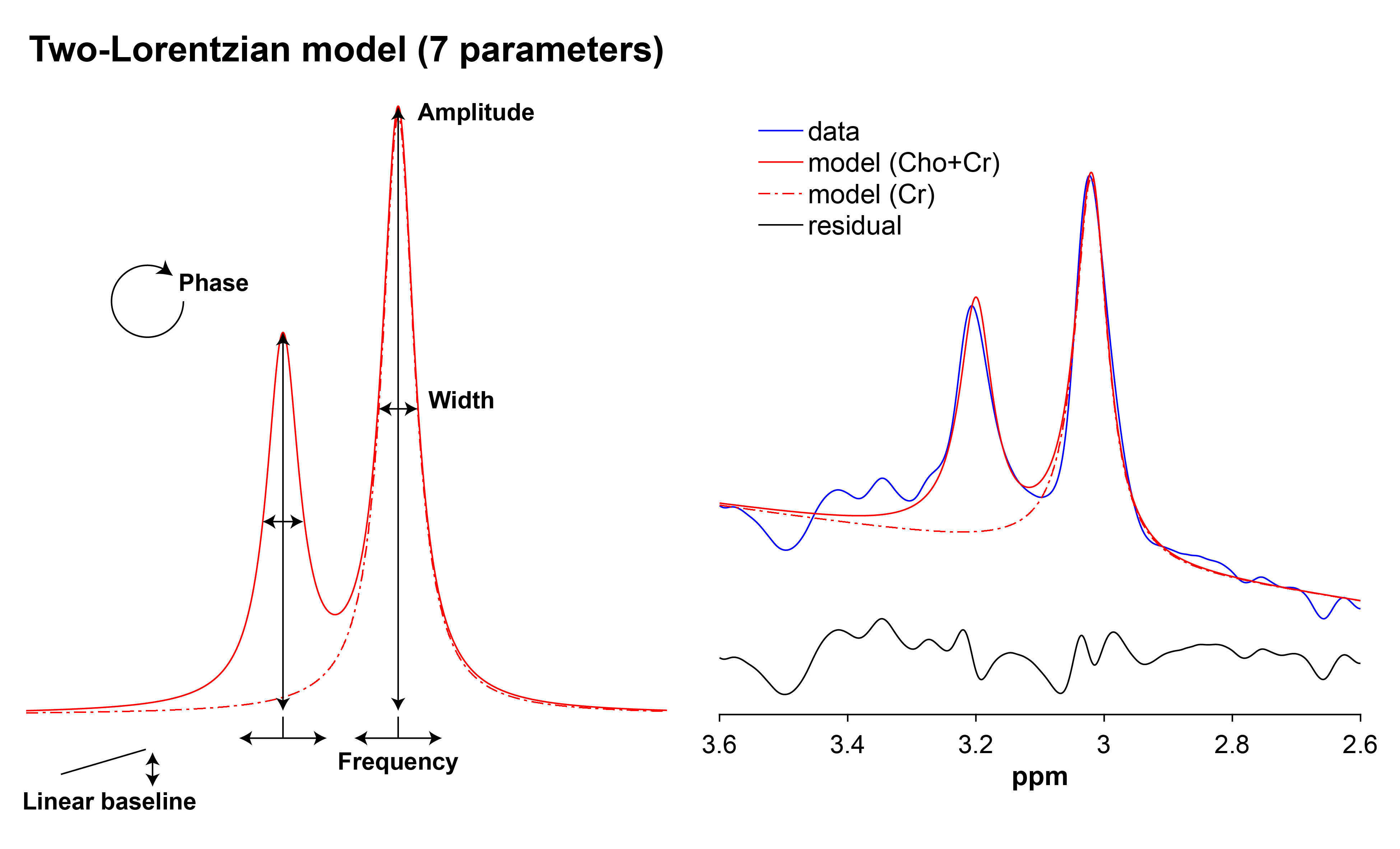
Cho and Cr in the edit-OFF spectrum are fitted with a two-Lorentzian model with a linear baseline:

\[ Absorption(f) = \frac{A}{2\pi}\frac{\gamma}{(f-f_0)^2+\gamma^2}+ \frac{Ah}{2\pi}\frac{\gamma}{(f-f_0-0.18)^2+\gamma^2} \] \[ Dispersion(f) = \frac{A}{2\pi}\frac{f-f_0}{(f-f_0)^2+\gamma^2}+ \frac{Ah}{2\pi}\frac{f-f_0-0.18}{(f-f_0-0.18)^2+\gamma^2} \]

\[ S(f) = \cos(\phi)Absorption(f)+ \sin(\phi)Dispersion(f)+ m(f-f_0)+b \]

where:

Parameter	Definition
\(A\)	Amplitude of Cr peak
\(\gamma\)	Lorentzian width (half-width at half-maximum)
\(f_0\)	Center frequency of Cr peak
\(h\)	Amplitude scaling factor for Cho peak
\(\phi\)	Phase

NAA

NAA in the edit-OFF spectrum is fitted with a Lorentzian model with a linear baseline:

\[ Absorption(f) = \frac{A}{2\pi}\frac{\gamma}{(f-f_0)^2+\gamma^2} \] \[ Dispersion(f) = \frac{A}{2\pi}\frac{(f-f_0)}{(f-f_0)^2+\gamma^2} \]

\[ S(f) = \cos(\phi)Absorption(f)+ \sin(\phi)Dispersion(f)+ m(f-f_0)+b \]

Water

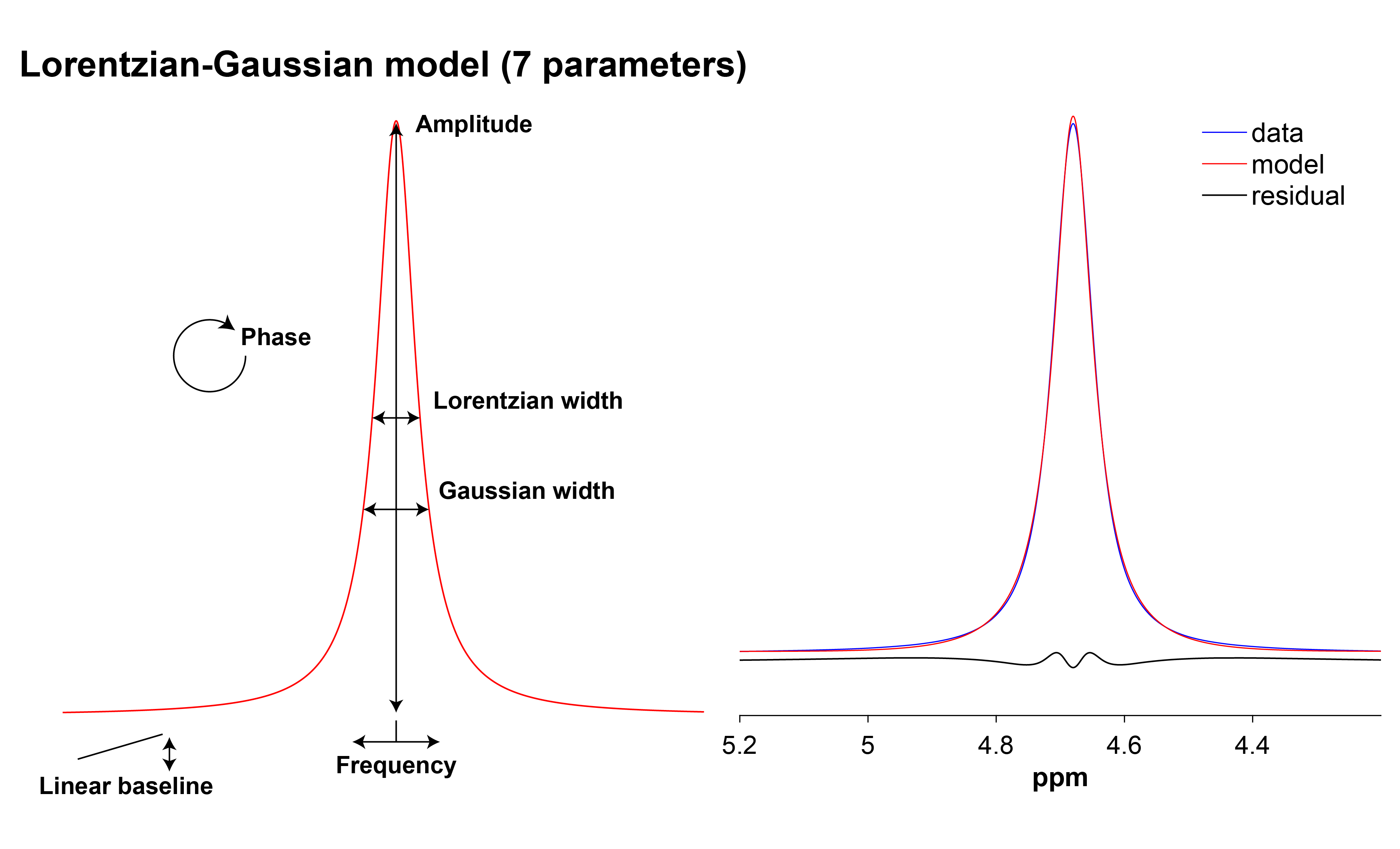
The unsurpressed water signal is fitted with a Lorentzian-Gaussian model with a linear baseline:

\[ S(f) = \frac{\cos(\phi)A+\sin(\phi)A\gamma(f-f_0)} {\gamma^2(f-f_0)^2+1} \exp[\sigma(f-f_0)^2]+ m(f-f_0)+b \]

References

1.

Evans CJ, Puts NAJ, Robson SE, et al. Subtraction artifacts and frequency (Mis-)alignment in J-difference GABA editing. Journal of Magnetic Resonance Imaging. 2013;38(4):970-975. doi:10.1002/jmri.23923

---

Built with R Markdown in RStudio

Copyright © 2020–2026, Mark Mikkelsen